Surveying is one of the most important activities in civil engineering. It helps in preparing maps, planning roads, bridges, railways, and irrigation systems. Different types of surveying methods are used depending on the project requirements. One such method is tacheometric surveying.
In simple words, tacheometric surveying is a type of surveying in which horizontal and vertical distances are measured indirectly using an instrument called a tacheometer. Unlike chain or tape methods, this process does not require direct measurement of distances. This makes it faster, especially in rough or hilly areas.
This article explains tacheometric surveying in civil engineering, its definition, instruments, principles, methods, applications, and advantages. The content is written in simple English for better readability and specially polished for Indian students, site engineers, and professionals.
Definition of Tacheometric Surveying

Tacheometry (also called tachemetric surveying) is a method of surveying where both horizontal distance and vertical elevation are determined without using a chain or tape. Instead, a tacheometer, which is a modified transit theodolite, is used.
This method is useful in places where direct measurement is difficult, such as:
- Steep slopes
- River valleys
- Uneven terrain
- Forest areas
In India, tacheometric surveying is often used in road alignment, railway projects, irrigation canal works, and contour mapping.
Principle of Tacheometric Surveying
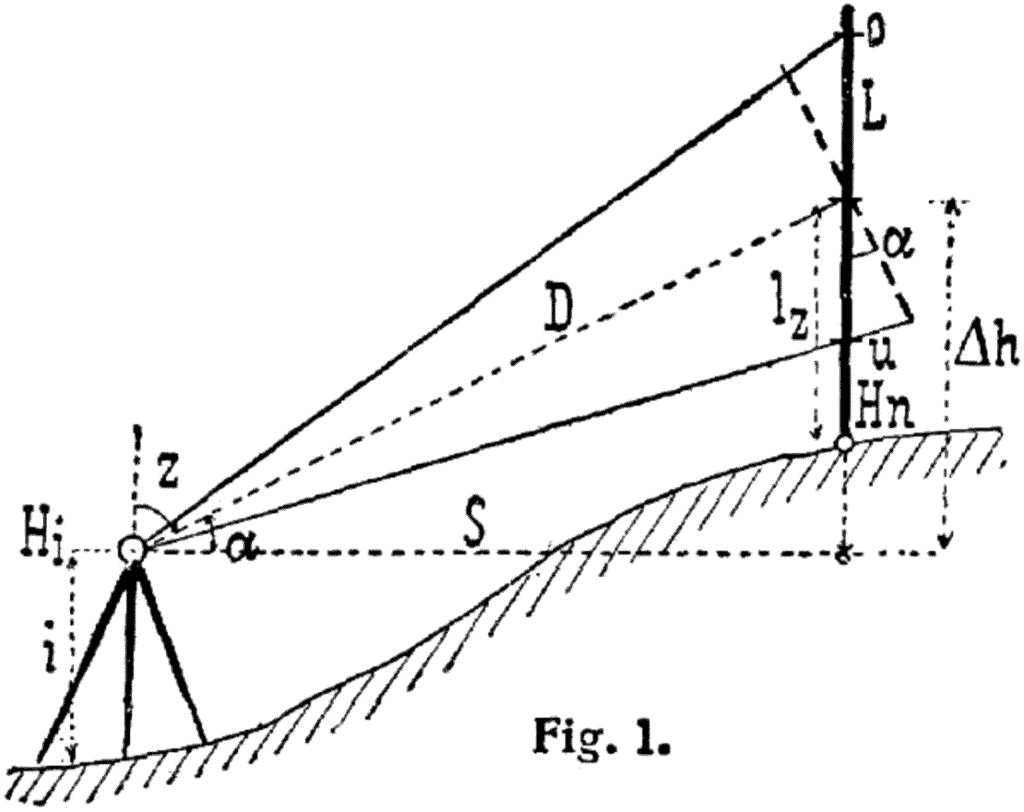
The principle of tacheometry is based on the stadia system. The instrument has stadia hairs (two additional horizontal hairs above and below the central cross-hair) in its telescope.
When a staff is held vertically on the ground, the distance between the readings cut by the stadia hairs gives a staff intercept. This intercept is then multiplied by a constant to calculate the horizontal distance.
Mathematically:
D = KS + C
Where:
- D = Horizontal distance between instrument and staff
- K = Multiplying constant (stadia constant)
- S = Staff intercept
- C = Additive constant (instrument constant)
This principle allows surveyors to measure long distances quickly without chaining.
Instruments Used in Tacheometric Surveying

The main instrument used is the tacheometer, which is basically a theodolite with some special features.
Features of a Tacheometer:
- Telescope fitted with stadia hairs.
- Magnification strong enough to read staff intercepts clearly.
- An anallactic lens may be fitted to remove the additive constant.
- Capable of measuring vertical as well as horizontal angles.
Other accessories include:
- Stadia rod or staff – graduated staff held vertically.
- Tripod stand – to mount the instrument.
- Plumb bob and tape – for temporary adjustments.
Also Read Singly vs Doubly Reinforced Beam – Difference, Design, and IS 456 Guidelines for Civil Engineering
Important tacheometric constants
In the stadia system, the distance from instrument to staff is given by:
D = K × S + C
- S = staff intercept (upper – lower hair)
- K = multiplying constant = f/i (focal length / stadia interval)
- C = additive constant = f + d (focal length + distance from instrument axis to objective)
Many modern tacheometers are adjusted to keep K = 100 and C ≈ 0 for easy mental math. An anallactic lens can be used to eliminate the additive constant so the formula reduces to D = K × S.
Methods of Tacheometric Surveying
There are mainly three methods of tacheometry used in civil engineering:
1. Stadia Method
This is the most commonly used method. It works on the principle of stadia hairs.
- The staff intercept (difference between upper and lower stadia hair readings) is observed.
- Using the formula, horizontal distance is calculated.
- Suitable for contouring and topographic surveys.
2. Tangential Method
In this method, only two points on the staff are read using the central hair. The vertical angle is also measured.
- Useful when stadia hairs are not available.
- Calculations are slightly more complex.
- Mostly applied in hilly terrain.
3. Subtense Method
Here, a fixed length subtense bar is used instead of a staff. The angle subtended by this bar at the instrument station is measured.
- Simple and quick.
- Mainly used in reconnaissance surveys.
Also Read Beam Reinforcement Details in Construction — Complete Practical Guide for Indian Projects
Standard formulas you actually use (memory aid)
For a line of sight inclined at angle θ:
- Horizontal distance from instrument axis to staff station:
D = K S cos²θ + C cosθ - Vertical difference between instrument axis and staff point:
V = K S (sin 2θ)/2 + C sinθ - With an anallactic lens (C = 0):
D = K S cos²θ and V = (K S sin 2θ)/2.
These come from basic optics and geometry of the stadia system and are standard in Indian course notes.
Tip: When θ is small (near horizontal), cos²θ ≈ 1, and the quick check D ≈ K S works fine if C ≈ 0.
Applications of Tacheometric Surveying in India
Tacheometry is very useful in civil engineering projects in India where the terrain is uneven and direct measurement is difficult.
Common applications include:
- Road and highway surveys – to decide alignment in hilly regions.
- Railway projects – for curves and gradients.
- Irrigation canals – designing alignment and slopes.
- Contour mapping – for preparing topographical maps.
- Reservoir and dam projects – for capacity estimation.
- Town planning – to prepare layout maps.
Advantages of Tacheometric Surveying
- Speed – Distances and elevations can be measured quickly.
- Less manpower – Requires fewer assistants compared to chain survey.
- Useful in rough terrain – Works well in hilly and forested areas.
- Versatile – Provides both horizontal distance and elevation.
- Good for contouring – Very effective for preparing contour maps.
Disadvantages of Tacheometric Surveying
- Accuracy is less compared to precise methods like total station or GPS survey.
- Requires skilled surveyors to operate and calculate.
- Not suitable for very flat areas where chain survey is easier.
- Cannot completely replace modern electronic methods.
Difference Between Tacheometric Surveying and Other Surveying Methods
| Aspect | Tacheometric Surveying | Chain Survey | Plane Table Survey |
|---|---|---|---|
| Speed | Fast, indirect measurement | Slow, direct measurement | Moderate |
| Terrain suitability | Best for hilly/uneven areas | Flat terrain only | Moderate |
| Instruments | Tacheometer, stadia rod | Chain, tape | Plane table, alidade |
| Accuracy | Moderate | High for short distances | Moderate |
| Applications | Roads, railways, contour mapping | Small plots, boundary survey | Field sketches |
Modern Relevance of Tacheometric Surveying
In India, total station surveying and GPS surveying are becoming more common. However, tacheometric surveying still holds importance in teaching, training, and in projects where advanced equipment is not available.
It remains a cost-effective method for preliminary surveys in rural and hilly regions.
FAQs on Tacheometric Surveying
Q1. What is meant by tacheometric surveying?
It is a method of surveying where distances and elevations are measured indirectly using a tacheometer.
Q2. What are the main methods of tacheometric surveying?
The stadia method, tangential method, and subtense method.
Q3. What are the applications of tacheometry in India?
It is used in road surveys, railways, irrigation canals, contour mapping, and dam projects.
Q4. Which instrument is used in tacheometric surveying?
A tacheometer (a type of theodolite with stadia hairs).
Q5. Is tacheometric survey outdated?
It is less used today due to total stations and GPS, but still important in hilly and remote areas.
Conclusion – Importance of Tacheometric Surveying in Civil Engineering
Tacheometric surveying is a fast and efficient method of surveying used in civil engineering. It provides both horizontal and vertical measurements without direct chaining.
While modern tools like total stations and GPS have reduced its use, it still plays an important role in road alignment, irrigation projects, railway design, and contour mapping in India.
For Indian students and engineers, understanding tacheometry in civil engineering is essential because it is still part of academic curriculum and practical fieldwork in many government and private projects.